General Relativity

Einstein expanded on His theory of special relativity by including the effects of gravitation into relativity. General relativity, changed the way we view space, the way special relativity changed our view of time.

Equivalence Principle of General Relativity

Einstein postulates the principal of equivalence in general relativity to require that there is no detectable difference between inertial and gravitational mass (for small distances). [ref 115, pg 434] That is, objects in an accelerating reference frame, like within a rocket in deep space, will be equivalent to the effects of objects within the gravity field of a large mass, like a planet. This is also expected from classical physics; but general relativity takes it farther, by applying this principle to light as well.

By using a simple thought experiment, Einstein shows some rather surprising outcomes of this principle of equivalence. Imagine two rockets side by side in deep space. An astronaut in one of the spacecraft fires a laser through the window of the other. Depending on their relative motion, the astronaut in the second craft will observe different results.

General Relativity Thought Experiment

See the figures above. In figure 1, both spacecraft are traveling at the same speed, that is, they have the same inertial reference frame. The beam of light travels in a straight line as viewed by both observers. In figure 2, the second craft is traveling faster than the first. The astronaut in the second ship will perceive the light to be entering at an angle, since the ship moves upward relative to the beam as it travels. In figure 3, the second ship is accelerating relative to the first craft. In this case, the laser follows a curved path as perceived by the second observer due to the increasing velocity of the second ship. Since the light beam is traveling horizontally from its origin, and the second ships relative speed is the negative vertical component of the perceived path, the rocket's acceleration causes the the vertical component to increase as it proceeds through the second ship. In all three cases, however, the astronaut in the first ship perceives the laser to fire horizontally.

This thought experiment would work out the same if the laser was replaced by a bullet. It is the fact that light responds in the same way to acceleration, that is important in general relativity. Remember Einstein's principle of equivalence, that the accelerated reference frame of the rocket in figure 3 must be equivalent to a reference frame within a gravitational field producing the same acceleration. For this to be true then light would have to be curved by gravitational fields the same way it is in the accelerating rocket. This is a basic prediction of general relativity.

Remember that nothing can travel faster than light. If light takes a curved path and some other object is made to take a straight path then that object could out run light, violating the speed limit established by special relativity. Since that is not possible, light must indeed be taking the shortest path available, meaning it is space that is curved. There is no straight path available in the presence of a gravitational field. The field warps space around it, curving it through an additional dimension that we do not directly perceive. [ref 115, pg 435]

Warped Space-Time

If you are to measure the circumference of a circle having a large mass concentrated at its center, you would find that at a great distance that C~2πr, as expected. But as you measure at smaller radii, you find that C<2πr, because the space is stretched out in the radial direction near the center of mass. The effect is actually small, for familiar environments, like that within the Earth's gravity well, but for something with a very high density, like a black hole or a neutron star, the effect is quite large.

Universal Consequences of General Relativity

The fact that space can be curved at all came as a surprise to many, when first learning of Einstein's theory. These small effects near gravitating bodies might seem to only be a local phenomenon. But all forms of energy have mass, as found through special relativity, and all mass generates gravitational fields. The universe is filled with matter and energy. This permits the universe as a whole to have a global curvature, depending on its average density.

Now that we can see the qualitative reasoning for curved space-time, it is easier to understand the meaning of the equations of general relativity. Actually, we will only look at the solutions for special cases, as this is most meaningful for understanding the nature of the universe.

At large scales, beyond the scale of galaxy clusters, the average density of the universe is approximately the same in all directions. So for the universe having a uniform density, and no net energy flux, Einstein's tensor equations reduce to:
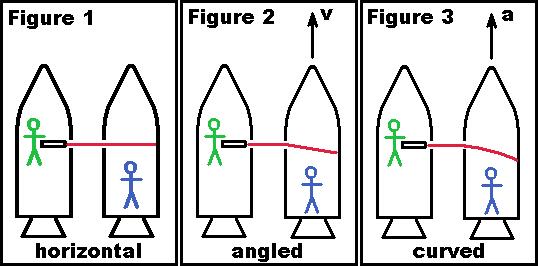
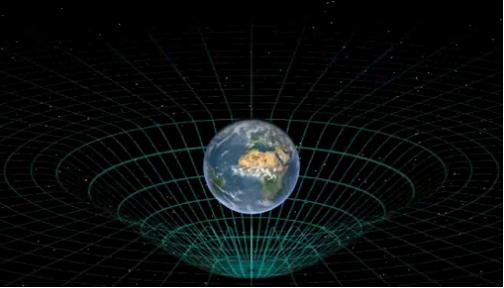
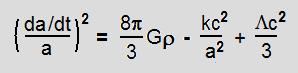
Equation 1: General relativity description of the universe

Equation 1: General relativity description of the universe

(Equation 1)

Equation 2: General relativity description of the universe

(Equation 2) [ref wiki, Friedmann Equations]

These equations are known as the Friedmann equations. Here 'a' represents the scale factor of the universe, that is, the relative size. By definition a=1 now, it varies with time and was smaller in the past. 'r' is the average energy density (including mass energy) of the universe, currently about 6 hydrogen atoms per cubic meter. This quantity also varies with time, inversely proportional to the cube of the scale factor. 'p' is the pressure, the universe contains particles which have pressure.

G, c, L, and k are constants. G is the gravitational constant. c is the speed of light in a vacuum. L is the cosmological constant, which represents the vacuum energy of empty space. It has been found to have a very small but non-zero value. The constant k represents the universal curvature of space. If k is positive then the universe has positive curvature and is finite in volume, taking the shape of a 3-sphere. If k=0, the universe is geometrically flat, and could have either finite volume (3-torus or other geometrically flat manifold) or infinite volume. If k is negative, then the universe has negative curvature and is infinite in volume. We do not know the exact value of k, but current observations suggest that it is either zero or nearly zero. Unfortunately, the difference between zero and nearly zero means we cannot tell if the universe is finite or infinite in size or know the shape of the universe.

For those with some basic knowledge of calculus, the formulas are not too difficult to understand. Lets start with equation 2. Note that the expression (d²a/dt²) is the second derivative of the scale factor, in other words, the acceleration of the rate of expansion or contraction of the universe. On the other side of the equation, only r and p are variable, but p is not very strong in our epoch, so we will only consider the effect of r here. The first term is negative and proportional to r. If the density (r) is large then this leads to a slowing of the expansion of the universe. This was the case early in the history of the universe, since the density was high. The second term contains the cosmological constant multiplied by the square of the speed of light. Though L is small, the speed of light is large, and the first term decreases with time as the density of universe decreases. Several billion years ago, this small constant began to dominate this equation, shifting the universe's expansion from deceleration to acceleration. Since the cosmological constant now dominates, and density continues to shrink, the expansion of the universe is expected to continue at an increasing rate forever.

The left side of the first equation is the square of the metric expansion of space in the universe. By metric, we mean on a per unit length basis. The quantity (da/dt)/a = H (Hubble's constant). This is the metric rate of expansion of the universe. From the second equation we see that the expansion rate is not constant but has decreased in the past and is increasing now. The total effect is that the current value of H is very near the average value it has had over the life of the universe. This allows us to easily estimate the universe's age (Age=1/H), which is now believed to be 13.8 billion years.

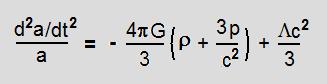
Return to General Science

Support Us: by liking us on Facebook or sharing our site with a friend. See the following links:

Visit us on Facebook

Share as Bookmark, Tweet, message, etc.

updated Jun 17, 2013
(c) 2013 RareUniverse.Org
(see our terms of service)